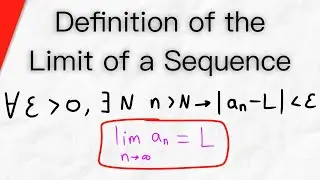Limits at Infinity and minus infinity. Real Analysis I. Bartle. Lec-89 (Urdu/Hindi) скачать в хорошем качестве

Limits at Infinity and minus infinity. Real Analysis I. Bartle. Lec-89 (Urdu/Hindi)

pdf notes of these video lectures can be down loaded from our google drive. https://drive.google.com/drive/folder... ************************************************************************************** To watch all videos of the playlist "Real Analysis I" visit the following:    • Real Analysis  I   ************************************************************************************ For more educational videos of maths visit our channel    / mathlogicpk   ********************************************************************************* In this part of lecture series course "Real Analysis I" Course of BS mathematics 5th Semester, we shall cover the following topics. Real Number System  Ordered sets, fields, the field of real numbers  Completeness property of R  The extended real number system  Euclidean spaces  Finite, countable and uncountable sets Sequences and Series  Sequences, subsequences, convergent sequences, Cauchy sequences  Monotone and bounded sequences, Bolzano Weierstrass theorem  Series, series of non-negative terms  Partial sums, the root and ratio tests, integral test, comparison test  Absolute and conditional convergence Limit and Continuity  The limit of a function  Continuous functions  Types of discontinuity  Uniform continuity  Monotone functions Differentiation  The derivative of a function  Mean value theorems, the continuity of derivatives  Taylor’s theorem Functions of Several Variables  Partial derivatives and differentiability, derivatives and differentials of composite functions  Change in the order of partial derivative, implicit functions, inverse functions, Jacobians  Maxima and minima Recommended Books 1. W. Rudin, Principles of Mathematical Analysis, 3rd edition, (McGraw Hill, 1976) 2. R. G. Bartle, Introduction to Real Analysis, 3rd edition, (John Wiley and Sons, 2000) ***********************************************************************************************