An Intuitive Introduction to Projective Geometry Using Linear Algebra скачать в хорошем качестве
Повторяем попытку...
Скачать видео с ютуб по ссылке или смотреть без блокировок на сайте: An Intuitive Introduction to Projective Geometry Using Linear Algebra в качестве 4k
У нас вы можете посмотреть бесплатно An Intuitive Introduction to Projective Geometry Using Linear Algebra или скачать в максимальном доступном качестве, видео которое было загружено на ютуб. Для загрузки выберите вариант из формы ниже:
-
Информация по загрузке:
Скачать mp3 с ютуба отдельным файлом. Бесплатный рингтон An Intuitive Introduction to Projective Geometry Using Linear Algebra в формате MP3:
Если кнопки скачивания не
загрузились
НАЖМИТЕ ЗДЕСЬ или обновите страницу
Если возникают проблемы со скачиванием видео, пожалуйста напишите в поддержку по адресу внизу
страницы.
Спасибо за использование сервиса ClipSaver.ru
An Intuitive Introduction to Projective Geometry Using Linear Algebra
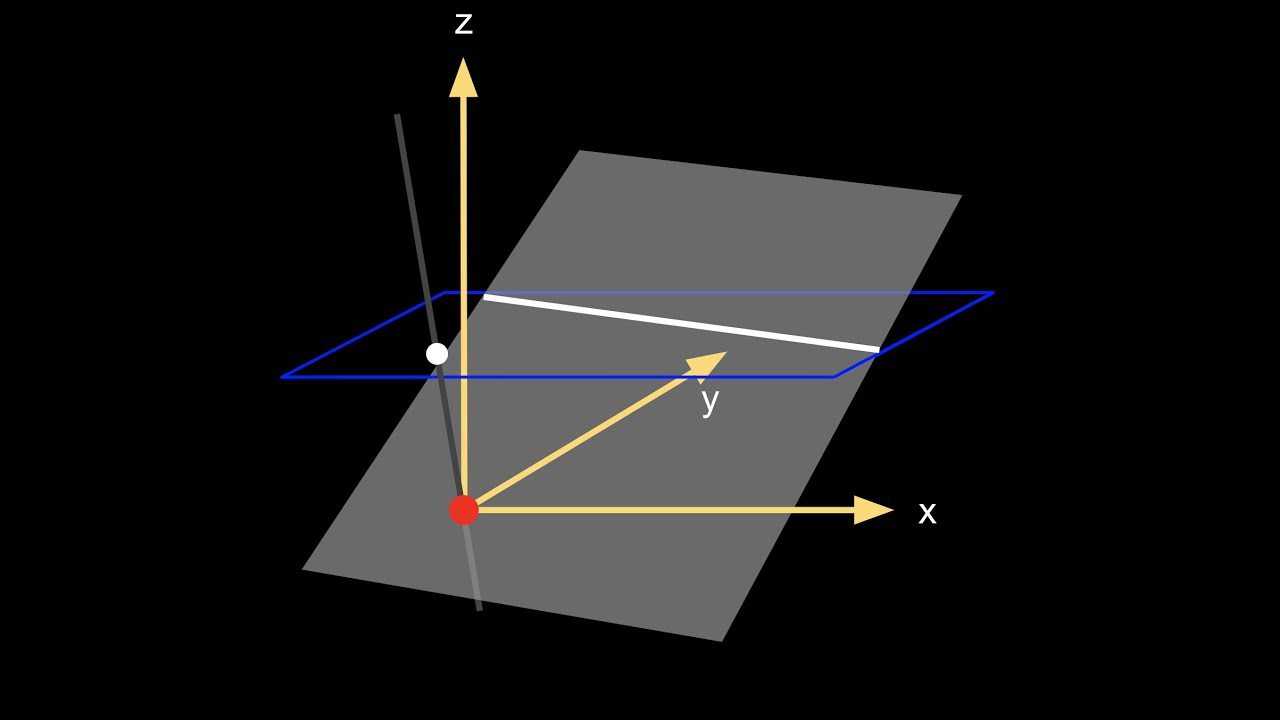
This is an area of math that I've wanted to talk about for a long time, especially since I have found how projective geometry can be used to formulate Euclidean, spherical, and hyperbolic geometries, and a possible (and hopefully plausible) way projective geometry (specifically the model that uses lines, planes, etc. through the origin) could have been discovered and not just created out of thin air. I am most likely not the first person to discover what I say in this video, but I have not found any sources that explicitly state the same things (except possibly NJ Wildberger with his video on how hyperbolic geometry is "projective relativistic geometry", which I haven't watched, but judging from the thumbnail it seems like he found the same connection between projective geometry and the Minkowski model of hyperbolic geometry that I make in this video). The first half of this video is intended for everyone; the second half (where I start talking about linear algebra) is intended for those who already know that subject on an introductory level, e.g. those who have taken a class in it or have watched 3Blue1Brown's series on it. Everything in this video comes from bits and pieces of articles and videos that I have sporadically watched over the last several (maybe 6 or 7) years, plus linear algebra that I have learned in a class I took more recently. As a result, I probably cannot give a complete list of all the sources I have used, but I will list as many as I can remember down below: Projective geometry: https://en.wikipedia.org/wiki/Homogen... • Projective geometry and homogeneous coordi... ("Projective geometry and homogeneous coordinates | WildTrig: Intro to Rational Trigonometry", Insights into Mathematics) Spherical geometry: https://en.wikipedia.org/wiki/Spheric... https://brilliant.org/wiki/spherical-... Hyperbolic geometry: https://en.wikipedia.org/wiki/Hyperbo... • Projection from Hyperboloid to the Beltram... ("Projection from Hyperboloid to the Beltrami–Klein disk.", Jamnitzer) https://dl.tufts.edu/concern/pdfs/bk1... ("Hyperbolic Geometry on a Hyperboloid", William F. Reynolds) https://www.roguetemple.com/z/hyper/m... ("Models and projections of hyperbolic geometry", Rogue Temple) 2D and 3D plots were made with Desmos and GeoGebra, respectively. All other images were made by me in Google Slides. Chapters: PART 1 0:00 Intro 0:31 Defining projective points and lines 4:19 Spatial coordinates 7:11 Projective quadratics 8:40 Non-Euclidean geometries 10:52 Distance metrics 12:11 PART 2 (linear algebra) 12:33 Defining projective points, lines with linear algebra 13:47 clmspace vs. nullspace representation of projective linear objects (points, lines, planes, ...) 16:32 clmspace to nullspace representation of a projective line (includes cross product) 20:31 Spans of clmspaces and interseections of nullspaces 21:33 3D projective geometry 23:13 Projective quadratics and double-cones 26:34 Summary #SoME2









![Визуализация всех возможных пифагоровых троек [3Blue1Brown]](https://image.4k-video.ru/id-video/T0GOz-Eqxl4)









