Convolution Integral: Solving Example and Understanding its Solution | Signals and Systems скачать в хорошем качестве
Повторяем попытку...
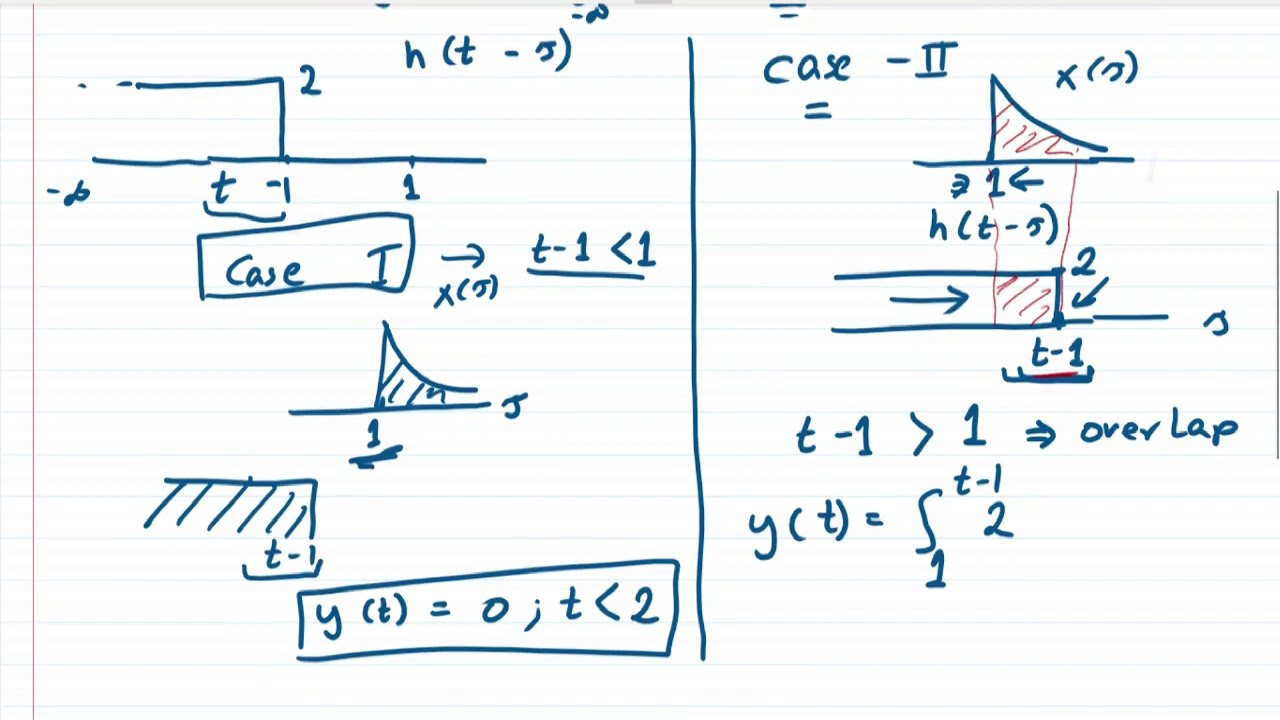
Скачать видео с ютуб по ссылке или смотреть без блокировок на сайте: Convolution Integral: Solving Example and Understanding its Solution | Signals and Systems в качестве 4k
У нас вы можете посмотреть бесплатно Convolution Integral: Solving Example and Understanding its Solution | Signals and Systems или скачать в максимальном доступном качестве, видео которое было загружено на ютуб. Для загрузки выберите вариант из формы ниже:
-
Информация по загрузке:
Скачать mp3 с ютуба отдельным файлом. Бесплатный рингтон Convolution Integral: Solving Example and Understanding its Solution | Signals and Systems в формате MP3:
Если кнопки скачивания не
загрузились
НАЖМИТЕ ЗДЕСЬ или обновите страницу
Если возникают проблемы со скачиванием видео, пожалуйста напишите в поддержку по адресу внизу
страницы.
Спасибо за использование сервиса ClipSaver.ru
Convolution Integral: Solving Example and Understanding its Solution | Signals and Systems
Convolution integral is a mathematical operation that is used to express the relationship between two functions and is often used in signal processing and control systems. The convolution integral is represented by the symbol ∗ (asterisk) and is defined as the integral of the product of one function (f(t)) with a time-reversed and scaled version of another function (g(t)) over the entire range of time. The result of the convolution integral is a third function (h(t)) that describes how the shape of one function is modified by the other function. The convolution integral is used to model a wide range of systems and processes in various fields such as electrical engineering, physics, and control systems. It is particularly useful in the analysis of linear time-invariant systems, where the output is a convolution of the input and the impulse response of the system. It is also used in signal processing applications such as filtering, image processing, and audio processing. Solved example of continuous time convolution integral signals and systems is given in this video.



















