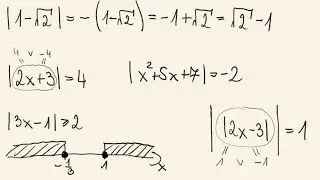Równania z wartością BEZWZGLĘDNĄ l Rozszerzenie l LICEUM скачать в хорошем качестве

Równania z wartością BEZWZGLĘDNĄ l Rozszerzenie l LICEUM

Temat: Równania z wartością bezwzględną — poziom rozszerzony [W opisie czeka MINI-QUIZ — sprawdź się po filmie! 🎯] „RÓWNANIA Z WARTOŚCIĄ BEZWZGLĘDNĄ (ROZSZERZENIE) 🔥 Trudniejsze przypadki krok po kroku! | Liceum” ——— Chcesz ogarniać trudniejsze równania z wartością bezwzględną: z dwiema wartościami, z sumą modułów, z parametrem i z liniową stroną? W tym filmie dostajesz klarowny schemat + sprytne triki, które działają zawsze — bez zgadywania i bez gubienia warunków. 🔹 Szybkie przypomnienie: interpretacja |x| jako odległości od zera i 3 sposoby startu (rozbicie na dwa równania, przypadki względem punktów krytycznych, metoda wykresowa). 🔹 Równania typu |ax + b| = c: kiedy rozwiązań brak (c ujemne), kiedy jedno (c równe 0), kiedy dwa (c dodatnie). 🔹 |ax + b| = |cx + d|: dwa równania A = B lub A = −B; kontrola warunków po rozwiązaniu. 🔹 Suma modułów: np. |x − p| + |x − q| = m — podział osi względem p i q, szybkie liczenie bez błędów. 🔹 Lewa wartość bezwzględna, prawa liniowa: np. |3x + 2| = 2x + 5 — najpierw warunek na prawą stronę (musi być nieujemna), potem przypadki. 🔹 Równania z parametrem (np. |x − a| = r): geometria na osi liczbowej i pełna klasyfikacja liczby rozwiązań. 🔹 Jak sprawdzać rozwiązania i wyłapywać „fałszywki” po przekształceniach. 🔹 Typowe pułapki: kwadratowanie bez kontroli warunków, gubienie znaku przy odwracaniu równań i „zjadanie” przypadków. Dla kogo jest ten film? 🔹 Dla uczniów liceum na poziomie rozszerzonym. 🔹 Dla osób szykujących się do sprawdzianu lub matury rozszerzonej z algebry. 🔹 Dla każdego, kto chce liczyć pewnie, szybko i bez wpadek. ——— MINI-QUIZ (Równania z wartością bezwzględną — rozszerzenie) 1. Rozwiąż równanie: |2x − 5| = |x + 4|. 2. Rozwiąż równanie: |x − 3| + |x + 1| = 6. 3. Rozwiąż w zależności od parametru m: |x − 2| = m − 1. Podaj, kiedy rozwiązań nie ma, kiedy jest jedno, a kiedy dwa. 4. Rozwiąż równanie: |3x + 2| = 2x + 5 (pamiętaj o warunku na prawą stronę). 5. Rozwiąż równanie z „podwójną” wartością bezwzględną: ||x − 2| − 3| = 1. ——— Jeśli chcesz więcej takich filmów, zostaw kciuk w górę i zasubskrybuj kanał — razem ogarniemy każdy dział! Napisz w komentarzu „ściąga”, jeśli chcesz krótkie podsumowanie do druku. #matematyka #liceum #rozszerzenie #wartośćbezwzględna #równania #algebra #matura LINK DO WSPARCIA KANAŁU:    / @matwujek   Wpadajcie do mnie na: @matwujek 🖥️ https://matwujek.pl 👾 Dc:   / discord   🎶 Tt:   / matwujek   📸 Ig:   / matwujek   Fb:   / matwujek   📧 @: [email protected] ——— ODPOWIEDZI DO MINI-QUIZU 1. Dwa równania: 2x − 5 = x + 4 lub 2x − 5 = −(x + 4). Otrzymujemy x = 9 lub x = 1/3. 2. Punkty krytyczne −1 i 3. Dla x mniejszego niż −1: 2 − 2x = 6 → x = −2. Dla przedziału od −1 do 3 suma wynosi 4, więc brak rozwiązań. Dla x nie mniejszego niż 3: 2x − 2 = 6 → x = 4. Zatem x = −2 lub x = 4. 3. Warunek istnienia: m − 1 nieujemne (czyli m co najmniej 1). • m równe 1 → jedno rozwiązanie: x = 2. • m większe niż 1 → dwa rozwiązania: x = 2 − (m − 1) oraz x = 2 + (m − 1). • m mniejsze niż 1 → brak rozwiązań. 4. Najpierw warunek: 2x + 5 nieujemne (x nie mniejsze niż −5/2). • Gdy 3x + 2 nieujemne: 3x + 2 = 2x + 5 → x = 3. • Gdy 3x + 2 ujemne: −(3x + 2) = 2x + 5 → −5x = 7 → x = −7/5. Oba rozwiązania spełniają warunek: x = 3 oraz x = −7/5. 5. Ustaw y = |x − 2|. Wtedy |y − 3| = 1, więc y = 4 lub y = 2. • |x − 2| = 4 → x = 6 lub x = −2. • |x − 2| = 2 → x = 4 lub x = 0. Razem: x = −2, 0, 4, 6.